[알고리즘/Java] BFS(너비우선탐색)과 DFS(깊이우선탐색) / Flood Fill (플러드 필) 알고리즘, 위상정렬(Topology sort)
BFS와 DFS는 그래프에서 모든 정점을 방문해야 할 때 정점을 방문하는 방법이다.
BFS(Breadth First Search)
너비우선탐색은 탐색 시작점의 인접한 정점들을 먼저 모두 차례로 방문한 후, 방문했던 정점을 시작점으로 하여 다시 인접한 정점들을 차례로 방문하는 방식이다.
인접한 정점들에 대해 탐색한 후 다시 너비 우선 탐색을 진행하기 때문에 선입선출 형태의 자료구조 큐를 활용
BFS알고리즘을 표현하자면
| BFS(v) //탐색 시작 정점 큐 생성 시작 정점 v를 큐에 삽입 정점 v를 방문한 것으로 표시 while(큐가 비어있지 않은 동안) u <- dequeue(Q); //큐의 첫번째 원소 반환 for each t : u의 인접 정점들 //u와 연결된 모든 정점들 if(!visited[t]) //방문한적 없는 정점이라면 정점 t를 큐에 삽입 정점 t를 방문한 것으로 표시 |
위와 같은 과정을 거친다.

위와 같은 그래프가 있고
이를 인접 행렬로 표현된 그래프를 BFS로 탐색한다면 아래와 같은 코드를 만들 수 있다.
// 들어갈때 방문 처리
static void bfs1() {
Queue<Integer> queue = new LinkedList<Integer>();
boolean visited[] = new boolean[N];
int current = 0;
queue.offer(current);
visited[current] = true; //들어갈때 방문처리
while(!queue.isEmpty()) {
current = queue.poll();
System.out.println((char)(current+65));
for(int i=0; i<N; ++i) {
if(adjMatrix[current][i] && !visited[i]) {
queue.offer(i);
visited[i] = true; //들어갈때 방문처리
}
}
}
}

처음 시작 상태는 위와 같다. 여기서 큐에 들어있는 A가 current로 나오고
A의 인접한 노드인 B와 C가 큐에 들어가게 된다면 Visited와 큐의 상태는 다음과 같이 변한다.

큐는 비어있지 않으므로 다시 while문을 돌게 되는데 이번 경우에는 current가 B가 된다.
B와 인접한 노드는 A, E, D인데 A는 이미 방문을 한적이 있으므로 큐에는 E와 D가 삽입된다.

이번 경우에는 C가 current로 바뀌고 C와 인접한 노드들이 큐에 들어 가게 된다.
C와 인접한 노드는 A와 E인데 이 둘은 모두 방문한 적이 있으므로 큐에는 아무것도 삽입되지 않고 이번 while문은 종료된다.

다음 경우 current는 D로 바뀌게 될것이다.D의 인접 노드는 B와 F인데 B는 이미 방문한적 있는 노드 이므로 F만 삽입되게 된다.
E의 경우에도 모든 인접 노드가 방문한적 있으므로 아무것도 큐에 삽입되지 않고 넘어가게 된다. F가 current가 되었을 때G가 큐에 삽입된다. 위와 같은 과정을 거치면 Queue는 비게 되고 while문을 빠져나오게된다.
방문 순서는 A-B-C-D-E-F-G가 된다.
DFS(Depth First Search)
시작 정점의 한 방향으로 갈 수 있는 경로가 있는 곳 까지 깊이 탐색해 가다가 더 이상 갈 곳이 없게 되면, 가장 마지막에 만났던 갈림길 간선이 있는 정점으로 되돌아와서 다른 방향의 정점으로 탐색을 계속 반복
가장 마지막에 만났던 갈림길로 되돌아가려면 재귀적으로 구현하거나 후입선출 자료구조인 스택을 사용한다.
재귀적으로 표현하면 다음과 같이 표현할 수 있다.
| DFS(v) v방문 표시 for each t : v에 인접한 정점들 if(!visited[t]) dfs(t); |
인접 리스트로 표현된 그래프를 DFS해보면 코드는 이렇게 된다.
static void dfs(int current,boolean[] visited) {
visited[current] = true;
System.out.println((char)(current+65));
for(Node temp = adjList[current]; temp != null; temp = temp.next) {
if(!visited[temp.vertex]) {
dfs(temp.vertex,visited);
}
}
}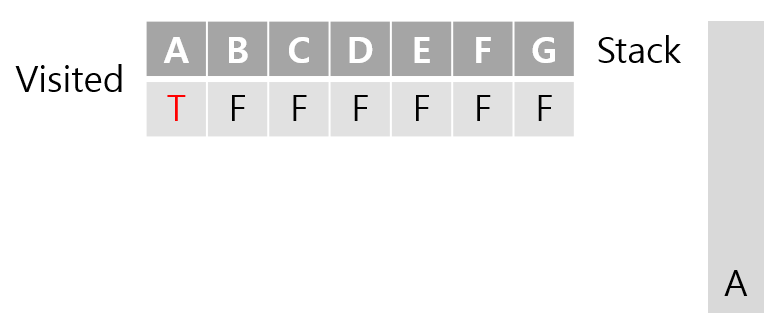
처음 메서드를 호출하게 되면 위와 같은 상태가 되고
for문을 통해 A와 인접한 노드 B, C가 불리게 된다.
우선 B가 먼저 불렸다는 가정하에 진행한다.
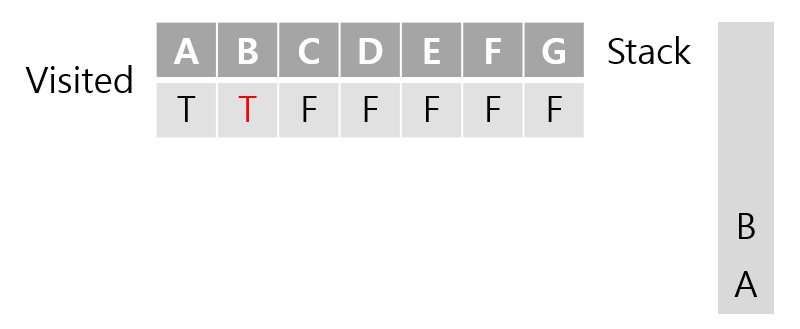
이번엔 B와 인접한 노드 A와 D와 E를 인자로 메서드를 호출할 차례이다. A는 이미 방문한적 있는 노드이므로 건너 뛰고 D가 먼저 호출되었다고 가정하에 진행한다.
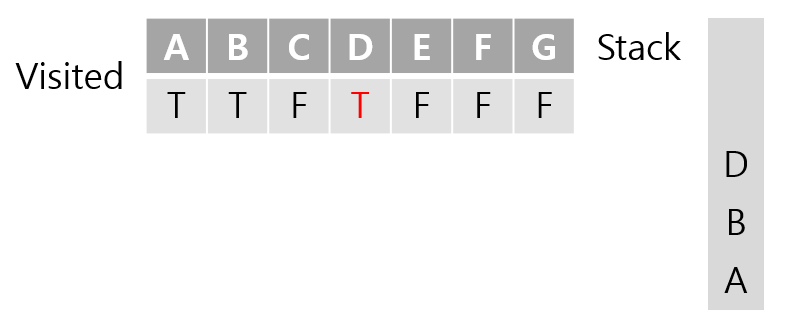
D와 인접한 노드는 B와 F가 있는데 B는 이미 방문한적 있는 노드이기 때문에 F를 방문하게 된다.
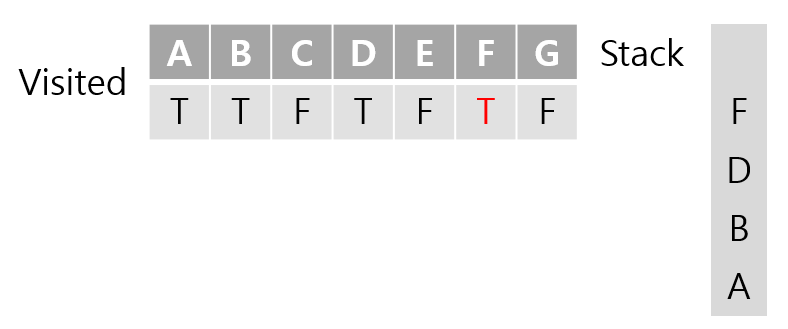
F와 인접한 노드는 D와 E와 G가 있다. D는 이미 방문한적 있는 노드이므로 E로 방문하게 된다.
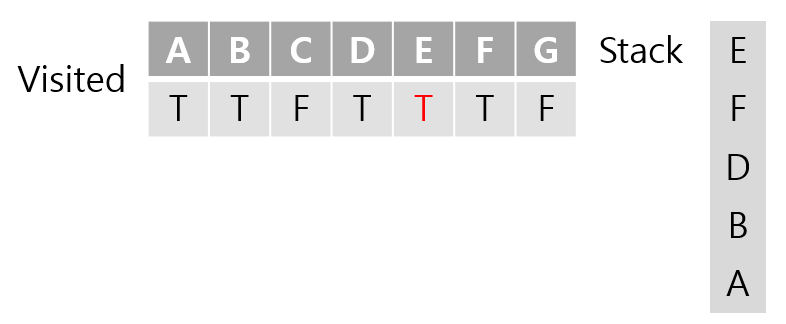
E와 인접한 노드는 B, F, C가 있다. 방문한적 있는 B와 F는 건너뛰고 C를 방문하게 된다.
C와 인접한 노드 A와 E는 모두 방문한적이 있는 상태가 되기 때문에 이전 호출 스택으로 return되게 된다.
E의 경우에도 가능한 모든 경우가 방문되었기 때문에 또 return되게 된다.
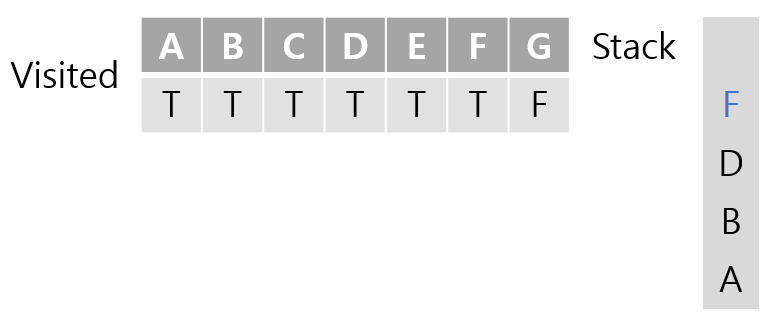
F와 인접한 노드 중 방문한적 없는 G로 방문하게 된다.
G가 스택에 들어온 경우에도 더이상 방문할 곳이 없기 때문에 계속해서 return되게 되면 처음으로 돌아가게되고 모든 정점을 방문한 상태가 됨을 알 수 있다.
방문 순서는 A-B-D-F-E-C-G로 BFS와 다른순서로 방문함을 알 수 있다.
Flood Fill
Flood Fill또는 seed fill이라고 하는 알고리즘은 다차원 배열의 어떤칸과 연결된 영역을 찾는 알고리즘이다.
주어진 시작점으로 부터 연결된 영역을 찾는다.
그림 프로그램에서 연결된 영역에 채우기 도구에 사용
지뢰찾기 같은 게임에서 비어있는 칸을 표시할 지 결정할 때 등에 사용
DFS와 BFS 모두로 구현이 가능하고 모서리가 맞닿은 칸이 연결되어있는지에 따라서 4방향과 8방향으로 나눌 수 있다.
4방향으로 탐색하는 경우는 아래 그림과 같다.

8방향으로 모서리부분을 넘어갈 수 있다면 아래와 같다.

아래 코드는 8방향으로 탐색하는 예시이다.
정사각형으로 이루어져있는 map이 주어지고 연결되지 않은 땅(1)하나를 섬으로 치고 섬의 개수를 출력하도록 하는 코드이다.
dr과 dc를 static변수로 선언해주어 8방향 탐색을 진행하고 dfs를 돌면서 방문한적 있는 땅은 0으로 바꾸어 다시 방문하지 않도록 처리했다.
public class FloodFillTest {
private static int R, C, map[][];
private static int[] dr = { -1, -1, -1, 0, 0, 1, 1, 1 }, dc = { -1, 0, 1, -1, 1, -1, 0, 1 };
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(in.readLine(), " ");
C = Integer.parseInt(st.nextToken());
R = Integer.parseInt(st.nextToken());
int cnt = 0;
map = new int[R][C];
for (int r = 0; r < R; ++r) {
st = new StringTokenizer(in.readLine(), " ");
for (int c = 0; c < C; ++c) {
map[r][c] = Integer.parseInt(st.nextToken());
}
}
for (int r = 0; r < R; ++r) {
for (int c = 0; c < C; ++c) {
if (map[r][c] > 0) {
cnt++;
dfs(r, c);
}
}
}
System.out.println(cnt);
}
}
private static void dfs(int r, int c) {
map[r][c] = 0;
int nr, nc;
for (int d = 0; d < 8; ++d) {
nr = r + dr[d];
nc = c + dc[d];
if (nr < 0 || nr >= R || nc < 0 || nc >= C || map[nr][nc] < 1)
continue;
dfs(nr, nc);
}
}
}
위상정렬(Topology sort)이란?
사이클이 없는 방향 그래프에서 노드 순서를 찾는 알고리즘이다.
위상 정렬은 순서가 정해져 있는 작업들을 차례대로 수행해야 할 때, 그 순서를 결정해줄 수 있다.
선후 관계가 정의된 그래프 구조 상에서 선후 관계에 따라 정렬하기 위해 위상 정렬을 이용할 수 있다.
정렬의 순서는 유행 그래프의 구조에 따라 여러 종류가 나올 수 있다.
위상 정렬이 존재하기 위해서는 반드시 그래프의 순환이 존재하지 않아야 한다.
BFS를 활용한 방법과 DFS를 활용한 방법 모두 가능하다.
BFS를 사용한 위상정렬
1.진입 차수가 0인 노드를 모두 큐에 넣는다.
2.큐에서 진입 차수가 0인 노드를 꺼내어 자신과 인접한 노드의 간선을 제거한다. -> 인접한 노드의 진입차수 1 감소
3.간선 제거 후 진입 차수가 0이 된 노드를 큐에 넣는다.
4.큐가 공백 상태가 될 때 까지 2-3을 반복한다.
java로 이를 구현하면 다음과 같이 할 수 있다.
Queue<Integer> q = new LinkedList<>();
for(int i = 1; i <= N; i++) {
if(edgeCount[i] == 0) {
q.add(i);
}
}
while(!q.isEmpty()) {
int now = q.poll();
//처리할 내용
for(int i = 0; i < students[now].size(); i++) {
edgeCount[g[now].get(i)]--;
if(edgeCount[g[now].get(i)] == 0) {
q.add(g[now].get(i));
}
}
}
DFS를 사용한 위상정렬
1.DFS를 위해 아무 정점이나 택한다.
2.위에서 선택한 정점으로 DFS를 진행하여 더 이상 전진할 수 없다면 연결리스트에 해당 정점을 삽입한다.
3.다시 1의 정점으로 돌아가 다음 탐색을 진행한다. 만약 더 이상 전진할 수 없다면 연결리스트에 해당 정점을 삽입한다.
4.더 이상 선택할 수 있는 정점이 없다면 아직 선택되지 않은 임의의 정점을 다시 선택하여 DFS를 진행해 1-3을 반복한다.
위를 반복하면 리스트에는 위상정렬의 역순으로 정점이 저장되어 있다.